Polar Coordinates

The polarcoord example generates 1000 random Cartesian 2D coordinates that are then converted to polar coordinates and printed to the terminal.

This is a very simple example but shows the concept of vertical versus horizontal vectorization quite nicely.

Background

In our problem we start with the allocation and random initialization of 1000 Cartesian 2D coordinates. Thus every coordinate consists of two floating-point values (x and y).

struct CartesianCoordinate
{
  float x, y;
};
CartesianCoordinate input[1000];

Cartesian coordinate

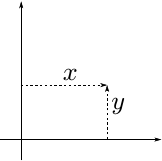
We want to convert them to 1000 polar coordinates.

struct PolarCoordinate
{
  float r, phi;
};
PolarCoordinate output[1000];

Polar coordinate

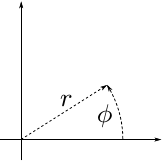
Recall that:

\[ r^2 = x^2 + y^2 \]

\[ \tan\phi = y/x \]

(One typically uses atan2 to calculate phi efficiently.)

Identify Vectorizable Parts

When you look into vectorization of your application/algorithm, the first task is to identify the data parallelism to use for vectorization. A scalar implementation of our problem could look like this:

for (int i = 0; i < ArraySize; ++i) {
  const float x = input[i].x;
  const float y = input[i].y;
  output[i].r = std::sqrt(x * x + y * y);
  output[i].phi = std::atan2(y, x) * 57.295780181884765625f; // 180/pi
  if (output[i].phi < 0.f) {
    output[i].phi += 360.f;
  }
}

The data parallelism inside the loop is minimal. It basically consists of two multiplications that can be executed in parallel. This kind of parallelism is already exploited by all modern processors via pipelining, which is one form of instruction level parallelism (ILP). Thus, if one were to put the x and y values into a SIMD vector, this one multiplication could be executed with just a single SIMD instruction. This vectorization is called vertical vectorization, because the vector is placed vertically into the object.

There is much more data parallelism in this code snippet, though. The different iteration steps are all independent, which means that subsequent steps do not depend on results of the preceding steps. Therefore, several steps of the loop can be executed in parallel. This is the most straightforward vectorization strategy for our problem: From a loop, always execute N steps in parallel, where N is the number of entries in the SIMD vector. The input values to the loop need to be placed into a vector. Then all intermediate values and results are also vectors. Using the Vc datatypes a single loop step would then look like this:

// x and y are of type float_v
float_v r = Vc::sqrt(x * x + y * y);
float_v phi = Vc::atan2(y, x) * 57.295780181884765625f; // 180/pi
phi(output[i].phi < 0.f) += 360.f;

This vectorization is called horizontal vectorization, because the vector is placed horizontally over several objects.

Data Structures

To form the x vector from the previously used storage format, one would thus write:

float_v x;
for (int i = 0; i < float_v::Size; ++i) {
  x[i] = input[offset + i].x;
}

Notice how the memory access is rather inefficient.

Array of Structs (AoS)

The data was originally stored as array of structs (AoS). Another way to call it is interleaved storage. That's because the entries of the x and y vectors are interleaved in memory. Let us assume the storage format is given and we cannot change it. We would rather not load and store all our vectors entry by entry as this would lead to inefficient code, which mainly occupies the load/store ports of the processor. Instead, we can use a little helper function Vc provides to load the data as vectors with subsequent deinterleaving:

Vc::float_v x, y;
Vc::deinterleave(&x, &y, &input[i], Vc::Aligned);

This pattern can be very efficient if the interleaved data members are always accessed together. This optimizes for data locality and thus cache usage.

Interleaved Vectors / Array of Vectorized Structs (AoVS)

If you can change the data structures, it might be a good option to store interleaved vectors:

struct CartesianCoordinate
{
  Vc::float_v x, y;
};
CartesianCoordinate input[(1000 + Vc::float_v::Size - 1) / Vc::float_v::Size];

Accessing vectors of x and y is then as simple as accessing the members of a CartesianCoordinate object. This can be slightly more efficient than the previous method because the deinterleaving step is not required anymore. On the downside your data structure now depends on the target architecture, which can be a portability concern. In short, the sizeof operator returns different values depending on Vc::float_v::Size. Thus, you would have to ensure correct conversion to target independent data formats for any data exchange (storage, network). (But if you are really careful about portable data exchange, you already have to handle endian conversion anyway.)

Note the unfortunate complication of determining the size of the array. In order to fit 1000 scalar values into the array, the number of vectors times the vector size must be greater or equal than 1000. But integer division truncates.

Sadly, there is one last issue with alignment. If the CartesianCoordinate object is allocated on the stack everything is fine (because the compiler knows about the alignment restrictions of x and y and thus of CartesianCoordinate). But if CartesianCoordinate is allocated on the heap (with new or inside an STL container), the correct alignment is not ensured. Vc provides Vc::VectorAlignedBase, which contains the correct reimplementations of the new and delete operators:

struct CartesianCoordinate : public Vc::VectorAlignedBase
{
  Vc::float_v x, y;
}
CartesianCoordinate *input = new CartesianCoordinate[(1000 + Vc::float_v::Size - 1) / Vc::float_v::Size];

To ensure correctly aligned storage with STL containers you can use Vc::Allocator:

struct CartesianCoordinate
{
  Vc::float_v x, y;
}
Vc_DECLARE_ALLOCATOR(CartesianCoordinate)
std::vector<CartesianCoordinate> input((1000 + Vc::float_v::Size - 1) / Vc::float_v::Size);

For a thorough discussion of alignment see Alignment.

Struct of Arrays (SoA)

A third option is storage in the form of a single struct instance that contains arrays of the data members:

template<size_t Size> struct CartesianCoordinate
{
  float x[Size], y[Size];
}
CartesianCoordinate<1000> input;

Now all x values are adjacent in memory and thus can easily be loaded and stored as vectors. Well, two problems remain:

1. The alignment of x and y is not defined and therefore not guaranteed. Vector loads and stores thus must assume unaligned pointers, which is bad for performance. Even worse, if an instruction that expects an aligned pointer is executed with an unaligned address the program will crash.
2. The size of the x and y arrays is not guaranteed to be large enough to allow the last values in the arrays to be loaded/stored as vectors.

Vc provides the Vc::Memory class to solve both issues:

template<size_t Size> struct CartesianCoordinate
{
  Vc::Memory<float_v, Size> x, y;
}
CartesianCoordinate<1000> input;

The Complete Example

Now that we have covered the background and know what we need - let us take a look at the complete example code.

#include <Vc/Vc>
#include <iostream>
#include <iomanip>

using Vc::float_v;

The example starts with the main include directive to use for Vc: #include <Vc/Vc>. The remaining includes are required for terminal output. Note that we include Vc::float_v into the global namespace. It is not recommended to include the whole Vc namespace into the global namespace except maybe inside a function scope.

int Vc_CDECL main()
{
    // allocate memory for our initial x and y coordinates. Note that you can also put it into a
    // normal float C-array but that you then must ensure alignment to Vc::VectorAlignment!
    Vc::Memory<float_v, 1000> x_mem;
    Vc::Memory<float_v, 1000> y_mem;
    Vc::Memory<float_v, 1000> r_mem;
    Vc::Memory<float_v, 1000> phi_mem;

At the start of the program, the input and output memory is allocated. Of course, you can abstract these variables into structs/classes for Cartesian and polar coordinates. The Vc::Memory class can be used to allocate memory on the stack or on the heap. In this case the memory is allocated on the stack, since the size of the memory is given at compile time. The first float value of Vc::Memory (e.g. x_mem[0]) is guaranteed to be aligned to the natural SIMD vector alignment. Also, the size of the allocated memory may be padded at the end to allow access to the last float value (e.g. x_mem[999]) with a SIMD vector. Thus, if this example is compiled for a target with a vector width (Vc::float_v::Size) of 16 entries, the four arrays would internally be allocated as size 1008 (63 vectors with 16 entries = 1008 entries).

    // fill the memory with values from -1.f to 1.f
    for (size_t i = 0; i < x_mem.vectorsCount(); ++i) {
        x_mem.vector(i) = float_v::Random() * 2.f - 1.f;
        y_mem.vector(i) = float_v::Random() * 2.f - 1.f;
    }

Next the x and y values are initialized with random numbers. Vc includes a simple vectorized random number generator. The floating point RNGs in Vc produce values in the range from 0 to 1. Thus the value has to be scaled and subtracted to get into the desired range of -1 to 1. The iteration over the memory goes from 0 (no surprise) to a value determined by the Vc::Memory class. In the case of fixed-size allocation, this number is also available to the compiler as a compile time constant. Vc::Memory has two functions to use as upper bound for iterations: Vc::Memory::entriesCount and Vc::Memory::vectorsCount. The former returns the same number as was used for allocation. The latter returns the number of SIMD vectors that fit into the (padded) allocated memory. Thus, if Vc::float_v::Size were 16, x_mem.vectorsCount() would expand to 63. Inside the loop, the memory i-th vector is then set to a random value.

Warning

Please do not use this RNG until you have read its documentation. It may not be as random as you need it to be.

    // calculate the polar coordinates for all coordinates and overwrite the euclidian coordinates
    // with the result
    for (size_t i = 0; i < x_mem.vectorsCount(); ++i) {
        const float_v x = x_mem.vector(i);
        const float_v y = y_mem.vector(i);

        r_mem.vector(i) = Vc::sqrt(x * x + y * y);
        float_v phi = Vc::atan2(y, x) * 57.295780181884765625f; // 180/pi
        phi(phi < 0.f) += 360.f;
        phi_mem.vector(i) = phi;
    }

Finally we arrive at the conversion of the Cartesian coordinates to polar coordinates. The for loop is equivalent to the one above.

Note

Inside the loop we first assign the x and y values to local variables. This is not necessary; but it can help the compiler with optimization. The issue is that when you access values from some memory area, the compiler cannot always be sure that the pointers to memory do not alias (i.e. point to the same location). Thus, the compiler might rather take the safe way out and load the value from memory more often than necessary. By using local variables, the compiler has an easy task to prove that the value does not change and can be cached in a register. This is a general issue, and not a special issue with SIMD. In this case mainly serves to make the following code more readable.

The radius (r) is easily calculated as the square root of the sum of squares. It is then directly assigned to the right vector in r_mem.

Masked Assignment

The phi value, on the other hand, is determined as a value between -pi and pi. Since we want to have a value between 0 and 360, the value has to be scaled with 180/pi. Then, all phi values that are less than zero must be modified. This is where SIMD code differs significantly from the scalar code you are used to: An if statement cannot be used directly with a SIMD mask. Thus, if (phi < 0) would be ill-formed. This is obvious once you realize that phi < 0 is an object that contains multiple boolean values. Therefore, the meaning of if (phi < 0) is ambiguous. You can make your intent clear by using a reduction function for the mask, such as one of:

if (all_of(phi < 0))  // ...
if (any_of(phi < 0))  // ...
if (none_of(phi < 0)) // ...
if (some_of(phi < 0)) // ...

In most cases a reduction is useful as a shortcut, but not as a general solution. This is where masked assignment (or write-masking) comes into play. The idea is to assign only a subset of the values in a SIMD vector and leave the remaining ones unchanged. The Vc syntax for this uses a predicate (mask) in parenthesis before the assignment operator. Thus, x(mask) = y; requests that x is assigned the values from y where the corresponding entries in mask are true. Read it as: "where mask is true, assign y to x".

Therefore, the transformation of phi is written as phi(phi < 0.f) += 360.f. (Note that the assignment operator can be any compound assignment, as well.)

Note

Vc also supports an alternative syntax using the Vc::where function, which enables generic implementations that work for fundamental arithmetic types as well as the Vc vector types.

Console Output

At the end of the program the results are printed to stdout:

    // print the results
    for (size_t i = 0; i < x_mem.entriesCount(); ++i) {
        std::cout << std::setw(3) << i << ": ";
        std::cout << std::setw(10) << x_mem[i] << ", " << std::setw(10) << y_mem[i] << " -> ";
        std::cout << std::setw(10) << r_mem[i] << ", " << std::setw(10) << phi_mem[i] << '\n';
    }

    return 0;
}

The loop iterates over the Vc::Memory objects using Vc::Memory::entriesCount, thus iterating over scalar values, not SIMD vectors. The code therefore should be clear, as it doesn't use any SIMD functionality.